6.4. A few words about convexity

Convexity is a remarkable structure which is ubiquitous in optimization.

6.4.1. Projection onto convex subsets in Hilbert spaces

Let \((H,\langle \cdot , \cdot \rangle)\) be a Hilbert space, with associated norm \(|| x || := \langle x,x \rangle^{1/2}\). The following result is the basis of many crucial properties of such a Hilbert space. Roughly, it expresses that when \(K \subset H\) is a closed and convex subset of \(H\), one may define a projection mapping \(p_K : H \to K\) which to each point \(x \in H\) associates the closest point \(p\) to \(x\) in \(K\), see Fig. 6.5.

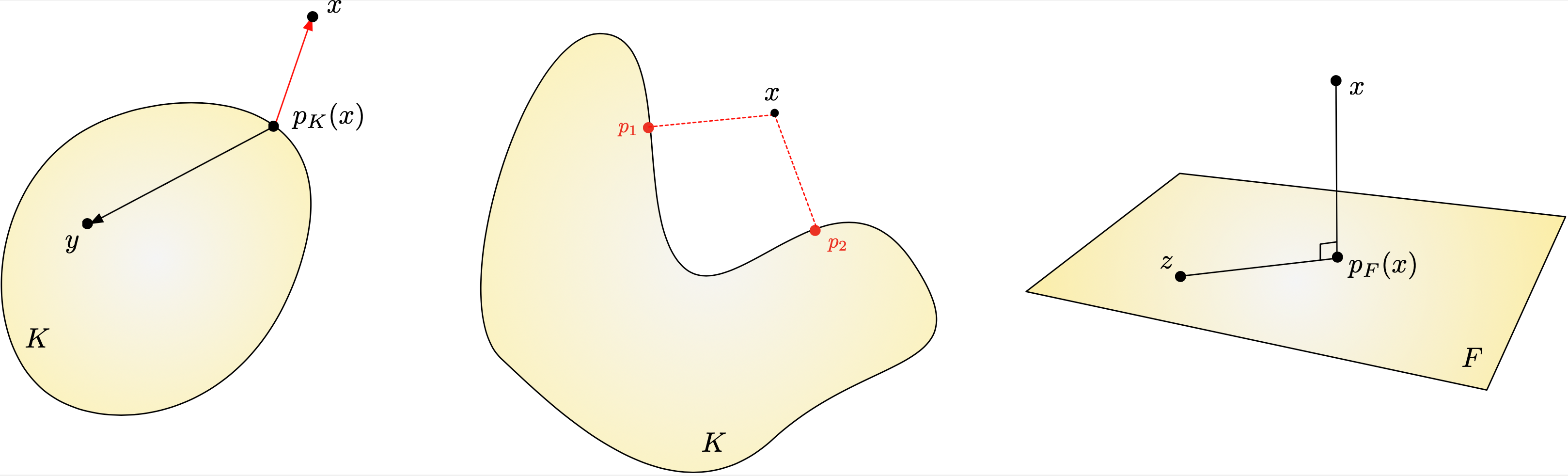
Fig. 6.5 (Left) Projection onto a closed convex set \(K\) in a Hilbert space; (center) When \(K\) is not convex, one point \(x \in H\) may have two closest points \(p_1\), \(p_2 \in K\); (right) Projection onto a closed vector subspace \(F\).

Theorem 6.7 (Projection onto a closed convex set)

Let \(K \subset H\) be a closed and convex subset. Then for all \(x \in H\), there exists a unique point \(p \in K\) such that

(6.2)\[\lvert\lvert x- p \lvert\lvert ^2 = \min\limits_{y\in K} \lvert\lvert x- y \lvert\lvert^2.\]

This point is called the projection of \(x\) onto \(K\) and it is denoted by \(p_K(x)\). It is characterized by the following fact:

(6.3)\[\begin{split}\forall z \in H, \quad z = p_K(x) \Leftrightarrow \left\{ \begin{array}{l} z \in K,\\ \forall y \in K, \:\: \langle z- x, y -z \rangle \geq 0. \end{array} \right.\end{split}\]

Eventually, the mapping \(p_K:H \to K\) thus defined is continuous.

Proof

Let us denote by

\[\delta = \inf\limits_{p \in K} \lvert\lvert x - p \lvert\lvert.\]

We do not know yet that this infimum is attained. However, from its definition, there exists a minimizing sequence for the problem, i.e. a sequence \(y_n\) of elements in \(K\) such that

\[\lim\limits_{n \to \infty}\lvert\lvert y_n - x \lvert\lvert = \delta.\]

We now use the Cauchy criterion to show that this sequence actually converges to an element in \(K\). To this end, we use the parallelogram identity in the Hilbert space \(H\); see Section 6.1.5. For all \(n, m \in \mathbb{N}\), we have

\[\begin{split}\begin{array}{ccl} \frac{1}{2} || y_n - y_m ||^2 &=& \frac12 || y_n - x - (y_m-x) || ^2 \\ &=& || y_n - x ||^2 + || y_m - x ||^2 - \frac12 || y_n + y_m - x ||^2 \\ &=& || y_n - x ||^2 + || y_m - x ||^2 - 2 \left\lvert \left\lvert x - \frac12(y_n + y_m) \right\lvert\right\lvert^2 \\ &\leq& || y_n - x ||^2 + || y_m - x ||^2 - 2 \delta^2, \end{array}\end{split}\]

where we have used the definition of \(\delta\) in the last line, together with the fact that \(\frac12(y_n + y_m)\) belongs to \(K\) since this set is convex. Now, since \(\lvert\lvert y_n - x\lvert\lvert\) converges to \(0\) as \(n \to \infty\), the right-hand side of the above inequality converges to \(\delta\) as \(m,n \to \infty\), which proves that \(y_n\) is a Cauchy sequence in \(H\). It therefore converges to some \(p\in H\), and \(p\) belongs to \(K\) since this set is closed. At this point, we have thus proved that there exists at least one point \(p\) satisfying (6.2).

Let now \(p \in K\) be any point satisfying (6.2), and let us prove that \(p\) also satisfies (6.3). For any point \(y \in K\), and for any \(t \in (0,1]\), the point \((1-t) p + ty\) belongs to \(K\), and so

\[|| x- p || ^2 \leq || x - (1-t) p - t y ||^2.\]

Expanding the right-hand side, we obtain that

\[|| x- p || ^2 \leq || x- p || ^2 - 2t \langle x-p, y-p \rangle + t^2 ||y-p ||^2.\]

Canceling the common term \(|| x- p || ^2\) in both side, dividing by \(t\) and then letting \(t\) tend to \(0\), we thus obtain the desired inequality

\[\langle x-p, y-p \rangle \leq 0.\]

At this point, we have thus proved that there exists at least one solution to (6.2), and that it satisfies (6.3).

Conversely, let \(z \in H\) be any point satisfying (6.3), that is:

\[z \in K \text{ and } \forall y \in K, \quad \langle z- x, y -x \rangle \geq 0.\]

Then, we have, for all \(y \in K\),

\[\begin{split}\begin{array}{ccl} || x - y || ^2 &=& || x- z ||^2 + 2 \langle x-z, z-y \rangle + || z-y ||^2 \\ &\geq& || x- z ||^2 + || z- y||^2. \end{array}\end{split}\]

Hence, it is clear that

\[\min\limits_{y \in K} || x-y ||^2 \geq || z- x ||^2,\]

and equality holds if and only if \(y = z\). Hence, \(z\) is the unique solution to the minimization problem (6.2). Since this argument holds for any point \(z\) satisfying (6.3), this shows in the meantime that there exists a unique such point \(z \in H\).

We have thus proved that there exists a unique solution \(p = p_K(x)\) to (6.2), which is equivalently characterized by (6.3). Eventually, we turn to the continuity of the (non linear) mapping \(p_K\). We actually prove that \(p_K\) is \(1\)-Lipschitz. For any two points \(x,y \in H\), let us write:

\[\begin{split}\begin{array}{ccl} || p_K(x) - p_K(y) ||^2 &=& \langle p_K(x) - p_K(y) , p_K(x) - p_K(y) \rangle \\ &=& \langle p_K(x) - x , p_K(x) - p_K(y) \rangle + \langle x-y , p_K(x) - p_K(y) \rangle + \langle y - p_K(y) , p_K(x) - p_K(y) \rangle \\ &\leq& \langle x-y , p_K(x) - p_K(y) \rangle , \end{array}\end{split}\]

where we have used the inequality (6.3) to pass from the second to the third line. Now, by the Cauchy-Schwarz inequality, we obtain:

\[|| p_K(x) - p_K(y) ||^2 \leq || x- y || || p_K(x) - p_K(y) ||,\]

which readily yields

\[|| p_K(x) - p_K(y) || \leq || x- y ||.\]

This shows the continuity of \(p_K\) and the proof of the theorem is complete.